Ｆａｓｃｉｎａｔｉｏｎ Ｎ−Ｄ−Ｆｉｌｅ　グラフ理論

グラフ理論は、数学の一分野。ノード（節点・頂点）の集合とエッジ（枝・辺）の集合で構成されるグラフの性質について研究する学問である。

コンピュータのデータ構造、アルゴリズムなどに広く応用されている。

グラフとは

例えば電車の乗り換え案内図を考える際には、駅（ノード）がどのように路線（エッジ）で結ばれているかが問題であって、線路が具体的にどのような曲線を描いているかは本質的な問題でないことが多い。

事実、乗り換え案内図を書く場合には、駅間の距離や微妙な配置、路線の形状といったものは、地理的な実際のそれとは異なって描かれることが多い。電車で移動する人を対象とした乗り換え案内においては、駅と駅の「つながり方」が主に重要なのである。

このように、「つながり方」に着目して抽象化された「点とそれをむすぶ線」の概念がグラフであり、グラフが持つ様々な性質を探求するのがグラフ理論である。

つながり方だけではなく「どちらからどちらにつながっているか」をも問題にする場合、エッジに矢印をつける。このようなグラフを有向グラフという。矢印のないグラフは、無向グラフという。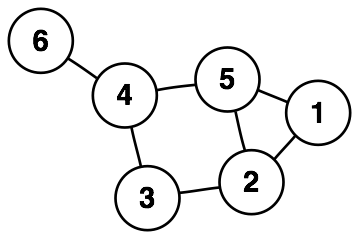

グラフの例

乗り換え案内図

前述の通り。

電気回路

回路図を書く場合、実際のリード線通りの形状に図を書いたりはしない。この場合も、「接点がどのようにつながれているか」だけが問題であって、「つながり方」を保ちつつできるだけ見やすい形に絵を描く。回路図は一種のグラフである。

WWWの構造

WWWにおけるウェブページの、リンク・被リンク関係がなす構造は、有向グラフの一種である。

グラフ理論の起源

グラフ理論は、1736年、「ケーニヒスベルクの問題」に対してオイラーが解法を示したのが起源とされる。この問題は、一筆書きと深く関連している。

厳密なグラフの定義

有向グラフ

V , E を集合とする。E の元に、二つのVを元の対で対応させる関数 f を

とすると、有向グラフ G は

G := (f, V, E)

と定義される。V をG の頂点(vertex)（またはノード）、E をG の辺(edge)（またはエッジ）と呼ぶ。

無向グラフ

P(V) を V のベキ集合とする。Eの元にV の 部分集合を対応させる関数 g を

とし、任意 e に対して g(e) = {v₁, v₂} のように値はちょうど二つの元の集合となっているとする。この時、無向グラフ G は

G := (g, V, E)

と定義される。V をG の頂点(vertex)（またはノード）、E をG の辺(edge)（またはエッジ）と呼ぶ。g の値が常にk > 2個の元の集合となっているとき、k-ハイパーグラフという。

E を最初からある集合の部分集合と考えれば、上の定義から関数を除くこともできる。有向グラフでは、E を V×V の部分集合、無向グラフでは、E を P(V) の部分集合で、二つの元の集合のみからなるものとすればよい。

グラフ理論の用語

グラフの定義によっては、辺に重み（コスト）が付いていることがある。このようなグラフは、重み付きグラフと呼ばれる。

グラフ G の頂点集合は V(G)、枝集合は E(G)で表すことが多い。

辺 e の両端の点を端点といい、端点は 辺e に接合しているという。また、辺と辺がある頂点を共有しているとき、その辺同士は隣接しているという。ある辺の両端点が等しいとき、ループ（自己ループ）という。また、2 頂点間に複数の辺があるとき、多重辺という。ループも多重辺も含まないグラフのことを単純グラフといい、ループや多重辺を含むグラフのことを多重グラフという。

二つのグラフ G と G' について、G' の頂点集合と辺集合が共に G の頂点集合と辺集合の部分集合になっているとき、G' は G の部分グラフであるという。逆に、G は G' の拡大グラフであるという。特に、頂点集合が等しい部分グラフのことを、全域部分グラフ（生成部分グラフ・因子）という。また、G の頂点集合 V の部分集合 S を取り出して、両端点が S に属する全ての辺を辺集合とする G の部分グラフを、誘導部分グラフという。それから、グラフ G からある辺を取り除き、その辺の両端点を一つの頂点に縮約したとき、縮約グラフ（商グラフ）という。

有向グラフにおいて、ある頂点 v に入ってくる枝の数のことを入次数、出て行く枝の数のことを出次数という。そして、頂点 v に接続する枝の数を次数といい、d(v) で表す。すべての v について、d(v) = k が成り立つとき、 k-正則という。ある k について k-正則なグラフのことを正則グラフという。グラフ G 中の最小次数の頂点の次数を δ(G)、最大次数の頂点の次数を Δ(G) で表すことが多い。また、次数 0 の頂点のことを孤立点という。

隣接している頂点同士をたどった v₁, e₁, v₂, e₂, ..., e_n-1, v_n の系列を歩道（鎖・ウォーク）という。辺の重複を許さない場合、路（小径・トレイル）といい、頂点の重複も許さない場合、道（パス（開いた歩道をパスという場合は単純パス））という。また、始点と終点が同じ路のことを閉路（回路・サーキット、サイクル）、始点と終点が同じ道（つまりe₁, e₂, ..., e_n, e1という路でe_iが相異なるもの）のことを閉道（サイクル）という。

任意の 2 頂点間に枝があるグラフのことを完全グラフ（完備グラフ）という。n 頂点の完全グラフは、K_n で表す。また、完全グラフになる誘導部分グラフのことをクリークという。サイズ n のクリークを含むグラフは「n-クリークである」と言う。辺を持つグラフは必ず 2 頂点の完全グラフを含むので 2-クリークである。また n-クリークであって、直径が n 未満となるグラフを n-クランと言う。